5716. Карточные
домики
Славик
мечтает стать артистом оригинального жанра, поэтому постоянно упражняется в
манипуляциях с различными предметами. В последнее время всё своё свободное
время он посвящает построению карточных домиков. Ему уже удалось возвести домашний
четырёхэтажный домик, на который понадобилось 26 карт. А
на уроке технологии Славик сумел тайком от учителя продемонстрировать своё
мастерство одноклассникам, построив трёхэтажный домик всего из 15 карт.
“Творчество”
будущего артиста запечатлено на фотографиях ниже:

Теперь
Славика заинтересовал вопрос математического характера: сколько карт
потребуется, чтобы построить домик в n этажей?
Он
просит Вас помочь ему, ведь с математикой у Славика пока не всё гладко.
Вход. Одно целое неотрицательное
число n (n ≤ 108)
– количество этажей в домике, который планируется построить.
Выход. Выведите количество карт,
необходимое для постройки домика в n этажей.
|
Пример
входа |
Пример
выхода |
|
3 |
15 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
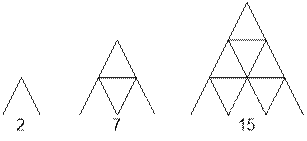
Пусть f(h) – количество карт, необходимых для построения карточного домика
высоты ![]() . Например, f(1) = 2, f(2) = 7, f(3) = 15.
. Например, f(1) = 2, f(2) = 7, f(3) = 15.
Чтобы построить домик
высоты h, в основании необходимо
установить h домиков высоты
1, на что
потребуется 2h карт, а также h – 1 перекрытий. На это основание затем устанавливается домик
высоты h – 1, для построения
которого требуется f(h – 1) карт.
Следовательно,
f(h) = 2h + h – 1 + f(h – 1)
или
f(h) = 3h – 1 + f(h – 1)
Выведем явную
формулу. Последовательно
раскрывая рекурсию, получим:
f(h) = 3h – 1 + f(h – 1) =
= 3h – 1 + 3(h – 1) – 1 + f(h – 2) =
. . .
= 3h – 1 + 3(h – 1) – 1 + 3(h – 2) – 1 + … + 3 * 1 – 1 =
= 3 (h + (h – 1) + (h – 2) + … + 1) – h =
= ![]() =
= ![]() =
= ![]()
Пример
Для домика высоты 1 достаточно 2
карты.
Для домика высоты 2 необходимо 7
карт.
Домик высоты 3 можно построить из
15 карт.
Реализация алгоритма
Читаем
высоту домика n.
scanf("%lld", &n);
Вычисляем
и выводим количество карт в домике.
res = n * (3 * n + 1) / 2;
printf("%lld\n", res);